חגים הם זמן טוב לשבור את השגרה ולעשות דברים קצת אחרת. אם יוצא לכם לנצל את הגישה הזו לטובת משפחה, תחביבים, חברים או משהו לנפש – זה נהדר, אבל זה נכון גם אם אתם עובדים במהלך החג.
בקמפוס למצוינות ברעננה מקיימים ברוב החגים סמסטר לימודים קצר ולא שגרתי. אני משתדל לנצל את המסגרת הזו כדי ללמד (וגם ללמוד בעצמי) נושאים מסוג שחורג למדי מאיזורי הנוחות שלי: במקום חידות, חשיבה וכישורים דיגיטליים אני מקדיש את רוב החגים לסדנאות של יצירה, בנייה, קיפול, צביעה ועוד מלאכות שאני אישית די בינוני בהן.
בשבוע חנוכה הזה החלטתי ללמד את הילדים איך לתכנן ולבנות גרסת-מיני של משחק הקלפים "דאבל" (Spot It). למקרה שפספסתם – בדאבל יש 55 קלפים עגולים, שבכל אחד מהם שמונה ציורים שונים. הקסם של המשחק הוא שבין כל שני קלפים שהשחקנים ישלפו במהלך המשחק יש צורה משותפת אחת בלבד, שאותה צריך לזהות במהירות.
פשוט ומורכב בו זמנית: פשוט לשחק, מורכב לתכנן. מאחורי הקסם הזה מסתתר חישוב מתמטי שמתבסס על תחום שנקרא "גיאומטריה פרוייקטיבית חיובית" (Finite Projective Geometry). אני לא יודע להסביר את החישוב הזה, אבל אם אתם בעניין – תוכלו לקרוא את ההסבר של "מדע גדול, בקטנה".
עכשיו מגיעה הקפיצה המתבקשת: איך מלמדים לתכנן משחק שאתה לא מבין את החישוב מאחוריו? התשובה היא שילוב בין פישוט של המשחק לבין בינה מלאכותית.
דאבל קטן פלוס
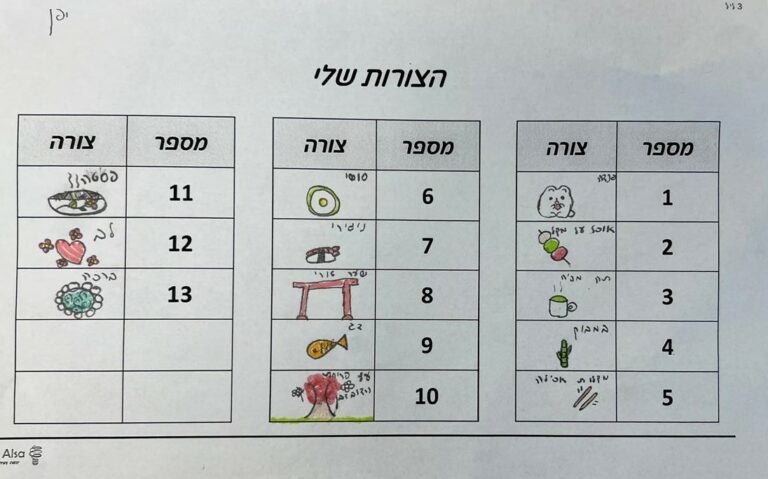
קודם כל, החלטתי שנייצר גרסה קטנה יותר של המשחק, כדי שיהיה לנו פרויקט שהילדים לא יתייאשו ממנו באמצע הדרך. רציתי שעל כל כרטיס יהיו רק 4 צורות שונות, והסתקרנתי לדעת כמה כרטיסים נדרשים כדי לייצר משחק ששומר על הכללים המקוריים של פיזור הצורות. כלי הבינה המלאכותית ניסו לעזור.
קלוד נתן לי תשובה מביכה; צ'אט ג'יפיטי ענה שנדרשים 13 קלפים ו- 13 צורות, אבל כשביקשתי ממנו לתאר את פריסת הצורות על כל כרטיס – היה קל לזהות שבין זוגות כרטיסים יש יותר מצורה אחת משותפת. נסיון שלישי עם פרפלקסיטי והופ – קיבלתי הסברים על אופן החישוב, מספר צורות נדרשות (13), מספר קלפים נדרשים (13) וחלוקה אלגנטית של הצורות בין הקלפים. אליפות!
כל אחד מהילדים התבקש לבחור נושא-על, לתכנן 13 צורות ולהשתמש במפתח פריסת הכרטיסים שסיפקתי להם כדי להכין לעצמו חבילת קלפי משחק אישית. מוזמנים להתרשם מהתהליך, כמו גם מהתוצאות הצבעוניות והמרגשות

דאבל בינוני
מרוצה מעצמי, החלטתי להגדיל את ההימור – כמה צורות וכמה קלפים צריך אם רוצים שעל כל קלף יהיו חמש צורות שונות? קלוד וצ'א גי'פיטי הפגינו עקביות עם תוצאות לא טובות. חזרתי לפרפלקסיטי, רפרפתי על התוצאה שהוא הציג לי והכנתי את הדפים שחולקו לילדים: 21 צורות ופריסה שלהן על פני 21 קלפים.
אופס!
מזל שהילדים יותר חכמים מהמורה.
"אלון, בין קלף 11 לקלף 18 אין צורה משותפת"
"ובין קלף 11 לקלף 15 יש שתי צורות משותפות"
אבוי לבושה. אנחנו תוך כדי שיעור. מה עושים?
ניסיון ידני אופטימי ראשון, שמבוסס על ההנחה המוטעית שרק צריך להחליף צורה אחת בין שלושת הכרטיסים הבעייתיים נוחל כשלון חרוץ.
דו שיח זריז וממוקד עם פרפלקסיטי, שבו פניתי ללב שלו, הצבעתי לו פרטנית על הבעיה, ביקשתי ממנו שיתחיל את כל הפריסה מחדש ואפילו ניסיתי להציע לו שוחד – והוא מסרב לעזור.
מה עושים? מחפשים ברשת עוד הסברים על המשחק, ובאחד האתרים מצאתי לא רק הסבר פרוייקטיבי בשפה מתמטית, אלא גם פריסה לגודל המשחק שרציתי.
הפעם השתמשתי בפרפלקסיטי רק כדי "לתרגם" את הפריסה שנוצרה על ידי אדם אמיתי לדף עבודה, ואפשר לחזור למהלך הרגיל של השיעור.
ותראו את התוצאות המרשימות לא פחות.
דאבל צ'ק
את המסר אתם יכולים להבין לבד – בינה מלאכותית היא סנדביץ': גורם אנושי צריך להגדיר לה מה הוא רוצה; היא יכולה לפעול באמצע עם כל הקסמים שלה; אבל בצד השני חייב לחכות גורם אנושי שיבדוק את התוצאות.
אני מסביר את העקרון הזה בלא מעט סדנאות, אבל הפעם נפלתי בו.
וטיפ אחרון – לא להתעצל, לבדוק פעמיים: דאבל צ'ק זה קסם.


