כולנו אוהבים לפתור חידות, אבל לא כולנו אוהבים חידות.
זה אומר שחלק מאתנו אוהבים חידות רק בתנאי שנצליח לפתור אותן.
היות שאני מתחיל את רוב השיעורים שלי במרכזי מחוננים ומצטיינים עם חידה אחת או שתיים – החלטתי לבדוק איך הילדים מנסים לגשר על התנאי הזה. ערכנו ביחד מיני-מחקר לא מבוסס מדעית במטרה לענות על השאלה "איך אני פותר/ת חידות" וגילינו כמה דברים ממש מעניינים. כל הילדים שבחרו להשתתף הם בכיתה ו'. הנה הצצה לתוצאות ולכמה דוגמאות מרתקות, ובסוף מצורפות גם שתי חידות שהילדים המציאו.
גישות שונות לפתרון חידות
השלב הראשון ב"מחקר" היה לכתוב את הדרכים המרכזיות שבהן הם פותרים חידות. הדוגמא שעליה התבססנו היתה כזו שכוללת סדרה של מספרים, ובמבט ראשון נראית כאילו הפתרון שלה הוא מתמטי. ברור שהוא לא! אני לא מלמד מתמטיקה. זה לא מפריע להם לנסות לחפש חוקיות מתמטית כלשהי ולנסות להוכיח שהיא נכונה…
שתי הדרכים המרכזיות שעלו בכל הקבוצות שהשתתפו היו "ניסוי וטעיה" ו"חישוב". זה די טבעי שאלו יהיו הגישות המרכזיות בחידות מהסוג הזה: הנירות המתמטית של החידה והאורינטציה האנליטית של חלק גדול מהילדות והילדים הביאו אותם גם לדרג את שתי הגישות האלו בתור הכי שימושיות. אם אני מזהה במבט חטוף את החוקיות – אני אנסה אותה. אם לא – אני אנסה למצוא אותה באמצעות חישוב. זה לא רק שימוש בכלים הכי חזקים שלי, אלא גם בחירה הגיונית לאור מה שנראה כמאפיינים של השאלה.
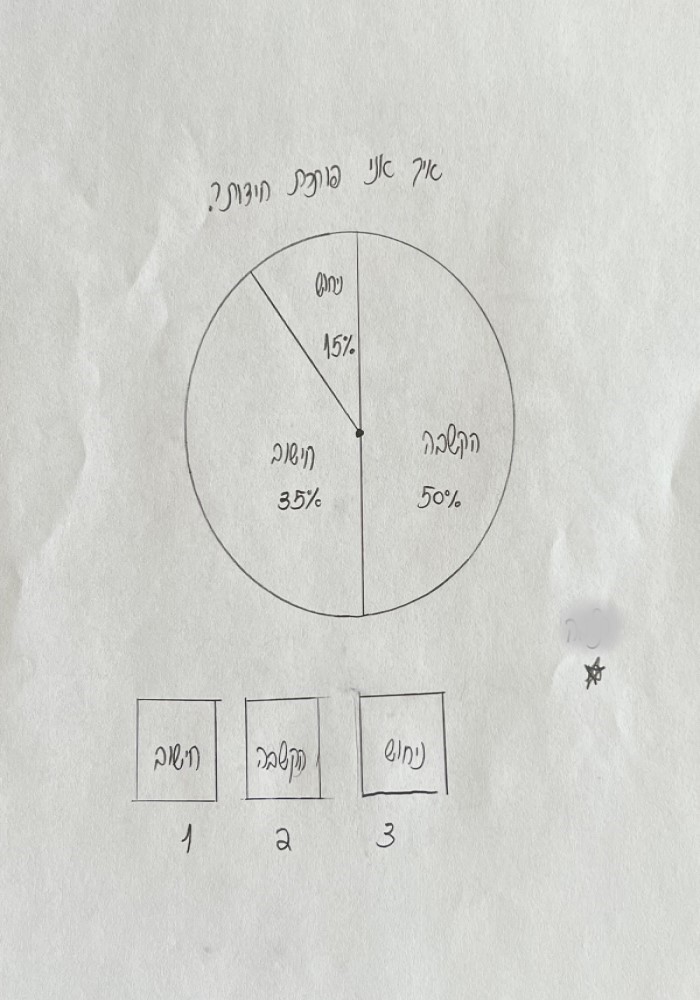
הנה שתי דוגמאות לקושי שהיה לחלקם להחליט איזו מבין שתי הגישות היא המועדפת עליהם. לא קשה לזהות את ההתלבטות עד הרגע האחרון ואת הבחירה המדויקת של האחוזים.
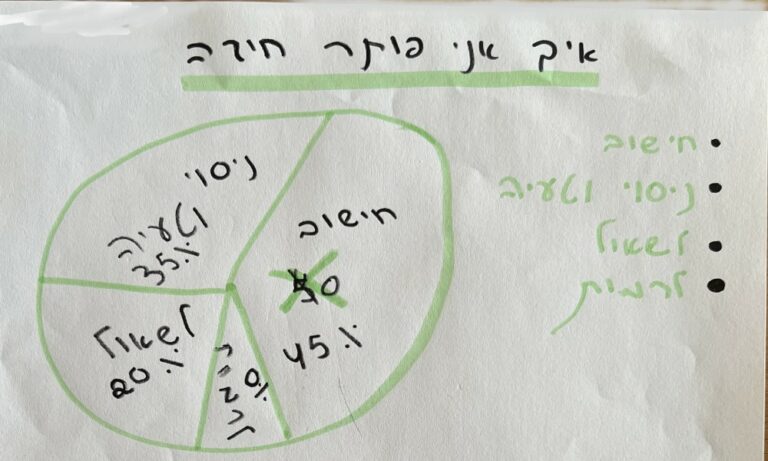
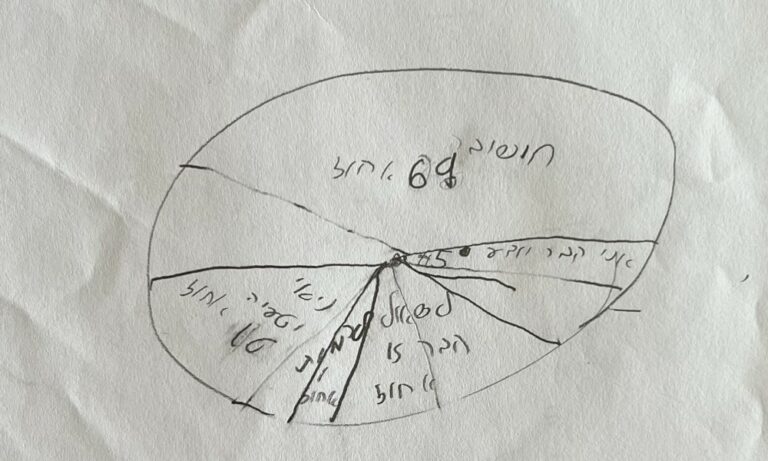
השם הרשמי של הגישה הראשונה הוא "נסייה וטעייה" – פתרון בעיות על ידי נסיונות מעשיים חוזרים ונשנים תוך תיקון הטעויות עד להצלחה. הסיבה לבחירה ב"נסייה" היא כדי להבחין בין הגישה הזו לבין ניסוי, אקספרימנט, מפני שלא מדובר בניסוי של ממש. על הדרך גם מתקבל משקל אחיד עם המילה "טעייה".
בשפת היומיום אנחנו משתמשים ב"ניסוי וטעיה". משחק הלשון "ניסוי ותהיה" הוא מקובל מאד ובעיניי יש לו קסם מיוחד, מפני שהוא ממחיש את תהליך הבירור הפנימי שאנחנו עושים עם עצמנו כדי להגיע לפתרון. כשמתחשק לי לחפור אני מוסיף גם את "ניסוי ותעיה", על משקל "לתעות ביער", שממחיש את המבוכה והבלבול שיכולה לאפיין את השיטה הזו.
אבל מה דעתכם על זה – ניסוי ותאיה? אני בעד להוסיף אותו לאפשרויות, כדי להראות שאם כבר מנסים כמה אופציות – צריך לשקול גם את הלא-הגיוניות!
אילו עוד שיטות לפתרון חידות הילדים העלו? היו לא מעט שבחרו ב"לשאול חבר" או "לשאול מישהו אחר"; היו שהוסיפו את "אני כבר יודע"; אני אהבתי את הכנות שמשתקפת אצל מי שהוסיף את "רמאות" ואפילו את אלו שסימנו את האפשרות הזו כזו שבה הם משתמשים הכי הרבה…
אבל אצל רובם, כל האפשרויות האחרות מלבד "ניסוי וטעיה" ו"חישוב" לא עלו על 25%.
אצל אף אחד מהם לא עלתה האפשרות של בדיקה שיטתית של כל האפשרויות אחת אחרי השניה. זה מעניין, כי זו אינדיקציה טובה לכך שאנחנו נוטים לדלג על האפשרות הזו במעבר בין שתי האפשרויות המובילות – היא נמצאת ממש ביניהן!
ילדים שונים, מאפיינים שונים
לצד התוצאות המעניינות, גם אם לא מבוססות מדעית, היה מרתק לראות עוד שני תחומים נוספים, שבהם ניכר הבדל משמעותי בין הילדים.
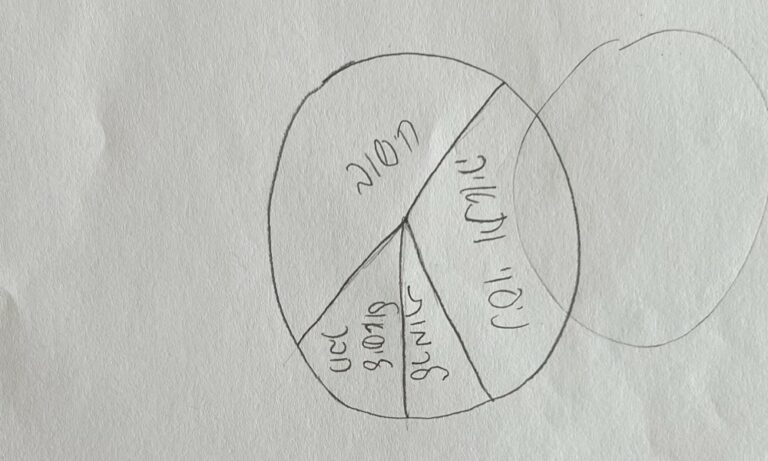
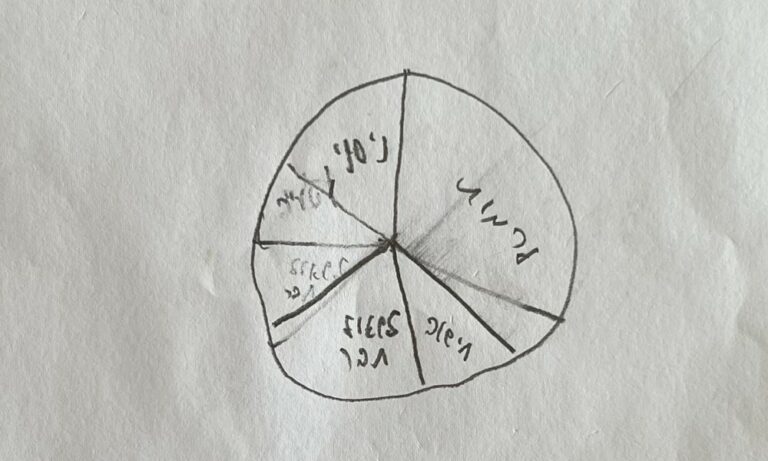
הראשונה היא מידת הדיוק שלהם בהצגת הנתונים: האם להשתמש בסרגל ובמחוגה? האם להשתמש בשנתות להצגת האחוזים? האם להשתמש בצבעים מבחינים לכל אפשרות פתרון? תראו את הדוגמאות המאלפות האלו ותחליטו בעצמכם האם הבחירה הזו חשובה לתוצר או לא.
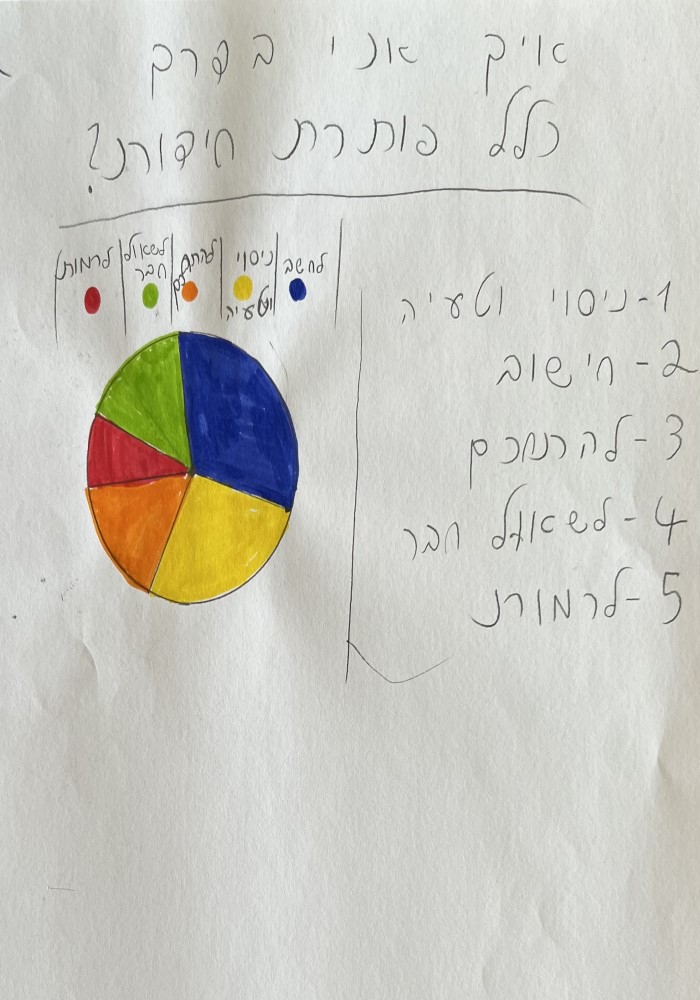
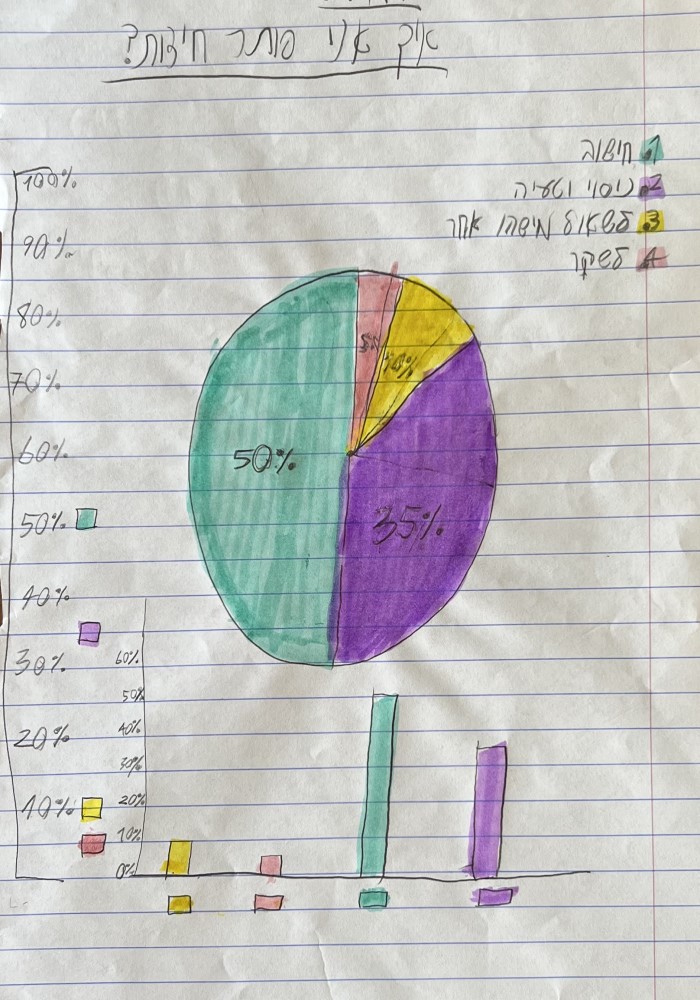
התחום הנוסף הוא האופן שבו הם התמודדו עם אלמנטים שהם לא מכירים (או לא מנוסים בהם), כמו הצגת תרשים עוגה או ייצוג של אחוזים בתוכה. במבט ראשון זה נראה כמו טעות משעשעת, או אולי אפילו מביכה.
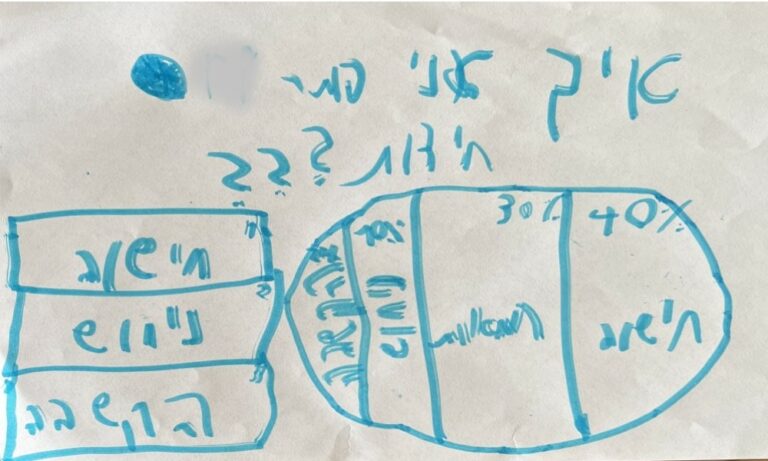
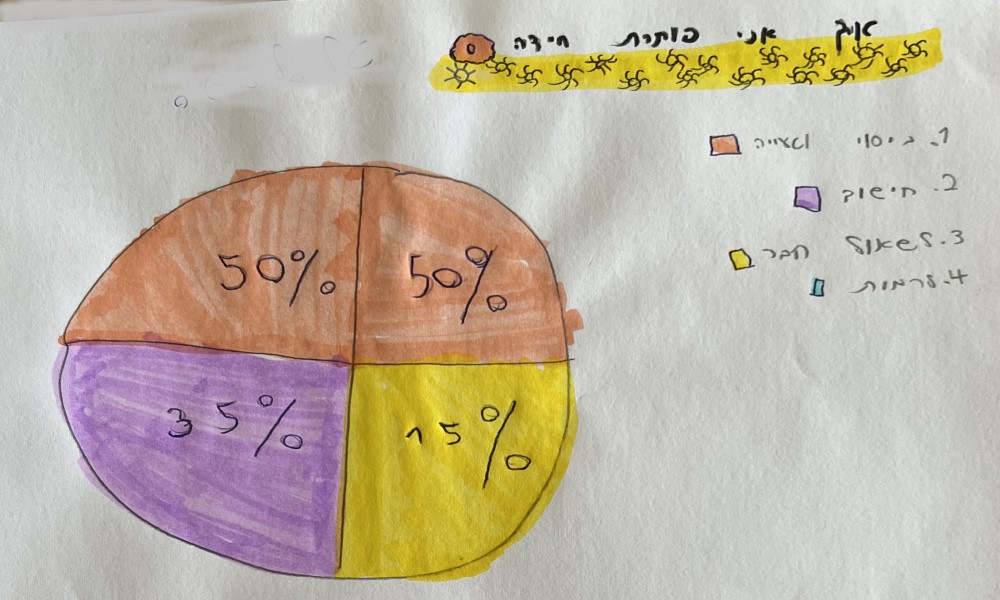
במבט שני, נזכרתי באותה פעם שבה כתלמיד בבית הספר יסודי התבקשתי לפתור תרגיל חילוק, לפני שלמדתי את שיטת החילוק הארוך. מתוך מצוקה או מתוך מחשבה יצירתית, כתבתי את תרגיל החילוק בשתי שורות – המחולק מעל המחלק, כמו בתרגיל חיבור או חיסור, ופתרתי את השאלה. המורה שלי אמנם טרחה לציין בציניות מסויימת ש"אלון המציא שיטה חדשה לתרגילי חילוק", אבל אני הייתחי גאה בעצמי מאד!
זו הסיבה שאני מזהה כאן את אלו שיכולים ומעזים לאלתר, להציג אלטרנטיבה אחרת ואינם מתביישים להגיש אותה. ככה נגלה צורות חדשות ומרגשות להצגת נתונים.
החידות שלהם
מה עם החידות שהבטחת, אתם שואלים?
אז הנה הן, בבקשה!
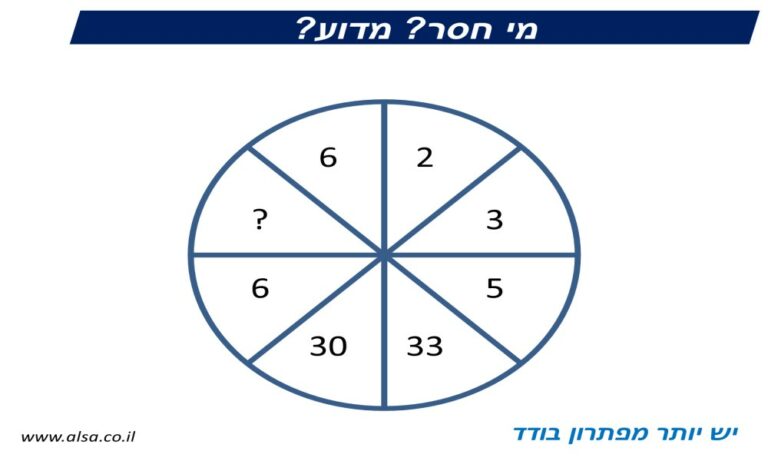
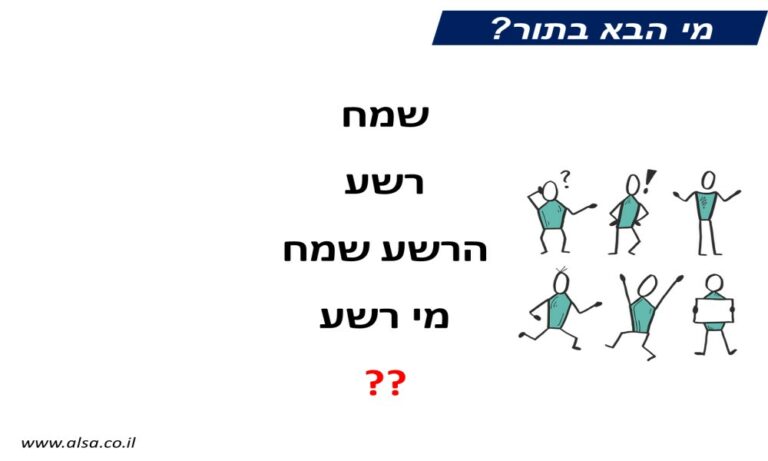
עד כאן להפעם.
