למי שעדין לא עשה את הקורס "ללמוד איך ללמוד" שמנחה ד"ר ננה אריאל במסגרת קמפוס IL – עזבו את הפוסט הזה ולכו להירשם כאן. הקורסים של קמפוס IL הם כולם מוצלחים ומהנים, הם מכסים תחומי ידע ועניין מגוונים מאד והם ערוכים נפלא, אבל את זה אהבתי במיוחד.
אם החלטתם להישאר ולקרוא, או שכבר עשיתם את הקורס, אז הנה משהו אחד מתוכו שעשה לי סדר באחד המרכיבים החשובים ביותר בלמידה, שרובנו מבינים באופן אינטואיטיבי אבל מסתבר שהוא גם מבוסס מחקרית: יש קשר ברור בין גוף לבין למידה.
בעיית מונטי הול ממשיכה לתעתע
אחת הבעיות הכי לא-אינטואיטיביות בסטטיסטיקה היא בעיית מונטי הול. היא קרויה כך על שמו של מנחה הטלויזיה שהנחה את השעשועון הוותיק Let's make a deal (עשינו עסק, בגרסה הישראלית). בסוף התכנית מציגים למתמודד שלוש דלתות – מאחורי אחת מהן יש מכונית ומאחורי שתי האחרות עז. הוא יכול לבחור איזו דלת לפתוח, אך כמובן שאינו יודע היכן המכונית.
הקטע הלא-אינטואיטיבי מגיע מיד אחרי שהוא בוחר באחת הדלתות. המנחה מציע לו להחליף את הדלת שבחר באחת משתי הדלתות האחרות. אם המשתתף יבצע את ההחלפה, האם הוא משפר את סיכוייו לזכות במכונית או שהסיכוי הוא 50% ולכן אין סיבה להחליף?
ספוילר: כדאי להחליף את הדלת שנבחרה. למה? יש לזה הסבר פשוט אבל מפתיע ולא טריוויאלי למח האנושי.
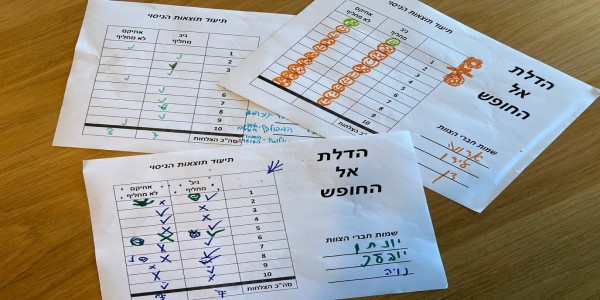
כשאני מלמד את הבעיה הזו אני מבקש מהמשתתפים לא לענות על השאלה בעל פה, אלא לבצע ניסוי שמדמה נסיון בריחה מהכלא. הם עובדים בצוותים: מנחה, משתתף שנשאר עם הדלת המקורית שבחר ומשתתף שמחליף את הבחירה. כל צוות חוזר על הניסוי 10 פעמים, כך שבמהלך השיעור יש לנו מדגם סטטיסטי מכובד שממחיש את הפתרון.
החלק הכי מעניין בשיעור הזה הוא שאני תמיד מבקש מהם שהניסוי יהיה "פיזי" – הם יכולים להשתמש בפתקים לייצוג הדלתות והמכונית, אבל הם יכולים להשתמש גם בכלי כתיבה, בחפצים שנמצאים סביבם או בנעליים שלהם (האופציה החביבה עליי…).
התוצאות לא רק מרשימות סטטיסטית, אלא גם המשתתפים זוכרים את תנועות היד של בחירת "הדלת" או ההחלפה שלה כחלק מנפילת האסימון והבנת פתרון הבעיה. עוד נחזור בהמשך לתנועת היד…
תיאוריית "הקידוד הכפול"
כמו רבים אחרים שמלמדים במסגרות שונות ומגוון גילאים, גם אני אוהב לגוון עד כמה שאפשר את התכנים ואת שיטות הלימוד. זה מאפשר לתקן ולהתאים אותם לקבוצות השונות, להטמיע פידבקים שקיבלתי וגם לא לשעמם את עצמי כשמדובר בשיעור שחוזר על עצמו.
באופן ספציפי, אנשי חינוך יודעים שכדאי תמיד לשלב מספר חושים בתהליך הלמידה, ולכן בהרבה שיעורים אנחנו משלבים דיבור עם טקסט, סרטונים עם חלק מפודקאסט, הרצאה עם התנסות מעשית של בניית מודל או יצירת מוצר מוחשי ועוד.
בעבר, תיאוריית "סגנונות הלמידה" הניחה שלכל אדם יש סגנון למידה שמתאים לתפיסה החושית הדומיננטית שלו. לפי הגישה הזו, יש אנשים שקל להם להבין ולתפוס באמצעות מידע כתוב או דימויים ויש מי שחייבים למשש כדי להבין על מה מדובר.
אבל מחקרים רבים בשנים האחרונות מראים שהתיאוריה הזו אינה נכונה. יש בינינו שונני באופן התפיסה של מידע, אבל זה לא אומר שלכל אחד יש סגנון ייחודי, ובוודאי שלא כדאי להסתמך רק על החוש הדומיננטי ללמידה.
תיאוריית "הקידוד הכפול" גורסת שכאשר משלבים בין חושים שונים וסגנונות למידה שונים – יכולת הלמידה משתפרת מאד. למעשה, לא מספיק לקלוט את המידע בשני חושים, אלא עדיף לבצע תהליך המרה אקטיבי בין החושים: לקרוא בקול טקסט כתוב, לכתוב הערות תוך כדי האזנה להרצאה וכו'.
עד כאן נשמע הגיוני, וגם די נפוץ כגישה חינוכית פרקטית מאד.
את ההרחבה המשמעותית של הקשר בין הגוף לבין הלמידה הבנתי מהסרטון שבו משוחחת ד"ר אריאל עם פרופ' דוד אהרונסון מבית הספר לחינוך בברקלי. אהרונסון עוסק בתחום של תודעה מעוגנת גוף. הוא טוען שאין שום תמיכה אמפירית לכך שקיימת חשיבה מופשטת שמנותקת מפעילות חושית או מוטורית. המטאפורה הרווחת של חשיבה שהמח מבצע בדומה לפעולה של מחשב מפספסת את תהליך הלמידה האמיתי, שהוא מעוגן בסביבה שלנו ובמה שאנו חשים.
כשמדברים על כמו תנועה, ריקוד, בישול וספורט קל להסכים שהלמידה קשורה מאד לחושים שלנו ולקשר שלנו עם הסביבה. אהרונסון מדגיש שכך מתרחשת תפיסה ולמידה גם במה שאנחנו חושבים כמופשט כמו פילוסופיה או מתמטיקה. כן, גם חשיבה מתמטית היא סנסורית ומוטורית.
בסרטון מתוארת, למשל, דוגמא של ניסוי שבו לימדו ילדים את המשמעות של חשיבה מכפלתית, שהיא מורכבת יותר להבנה מאשר חשיבה חיבורית (אדטיבית). הילדים התבקשו לייצר תנועה של עצמים על מסך על ידי הזזת שתי הידיים שלהם, באופן שמייצג יחס מכפלתי בין גובה הידיים (כלומר הן לא התרוממו באותו קצב). ניסוי כזה מייצר עבור הילד מודל פיזי של יחס מתמטי קשה להבנה!
ה"משוריבול" וגלגל ההצפנה
אני ממליץ בחום להאזין לשיחה כולה במסגרת כלל הקורס, אבל בואו נחזור לרגע לדוגמאות נוספות של שיעורים שלי, שפתאום ראיתי באור שונה.
כשאני מסביר לפעמים על זוויות מבט שונות שמאפשרות לראות דברים שונים, אני משתמש בצורה המופלאה "משוריבול" – כאשר תסתכלו עליה משלושה כיוונים שונים תראו משולש, ריבוע או עיגול. אני מקרין לפעמים את הסרטון המשעשע הזה מהסדרה "גיאומטריה: נא להכיר" של הטלוויזיה החינוכית, אבל לפעמים נותן לכולם לבנות בעצמם משוריבול מפלסטלינה ואפילו מעץ.

כשאני מלמד על צופן קיסר, שבו מחליפים את אותיות ה- א"ב באותיות אחרות לפי מפתח הזזה מוסכם מראש אני נותן למשתתפים לעשות זאת בתוך אתר אינטרנט אינטראקטיבי ידידותי ופשוט, אבל לפעמים גם נותן להם לגזור ולהרכיב בעצמם גלגל כזה.


בדיוק כמו הנעליים בשיעור על בעיית מונטי הול, עד היום ראיתי בבנייה ובהפעלה של החפצים בעיקר דרך להעשרת הלמידה, יצירת עניין, גיוון שיאפשר לכל אחד את הדרך המתאימה לו ביותר להבנה.
מהקורס "ללמוד איך ללמוד" ומהשיחה עם פרופ' אהרונסון אני מבין שיכול להיות שהבחירה בהם גם יכולה להיות דרך טובה יותר להבין את עצם המושגים המופשטים, בעיקר בעולם המתמטיקה, אבל לא רק בו.
אז מה האתגר הבא בתחום?
תקופת הקורונה הפגישה גם את מי ששונא מתמטיקה עם המושג הקשה לתפיסה "גידול אקספוננציאלי" או "גידול מעריכי". קל להסביר אותו במילים, אבל הרבה יותר קשה לתפוס את מלוא המשמעות שלו. הקריקטורה הזו הופצה כל כך הרבה פעמים בשנת 2020, ואפילו אילון מאסק צייץ אותה וכתב "בקרוב גם גרפים לוגריתמיים".
נכון, יש שיטות חצי-מוחשיות להסביר מה זה גידול אקספוננציאלי:
הסיפור על הקיסר, לוח השחמט וגרגרי האורז שמציג את המשמעות של גידול בחזקות 2
משחק החידה "משחקי האנוי", שבו הזמן להשלמת המשימה עולה בצורה מעריכית ככל שמספר הטבעות עולה).
ישנו גם ההסבר של יהלי אדמתי שמציגה מה ההבדל בין המרחק שנגיע אליו אם נלך 30 צעדים לבין המרחק שנעבור אם נלך 2 בחזקת 30 צעדים, אך קשה ליישם אותו בהתנסות מעשית..
האם יש דרך טובה יותר להסביר את המושג "אקספוננציאלי" למי שלומד אותו בפעם הראשונה, תוך ניצול הקשר בין הגוף לבין הלמידה?
עד כאן להפעם
